3-3. 負荷トルクの算出

駆動機構の条件をもとに、負荷トルクを算出します。
負荷トルクとは、駆動機構の接触部分に生じる摩擦抵抗に対して必要なトルクです。
負荷トルクの値は、必要トルクを算出に使用します。

負荷トルク（T_L）の求め方

ボールねじ駆動の計算式

タイミングベルト・プーリー駆動の計算式

• ※ インデックステーブル駆動では、摩擦抵抗が微小のため、負荷トルクの算出は省略します。（0とする）
  インデックステーブル駆動の機構仕様例で選定を進める場合は、3-4. 負荷慣性モーメントの算出に進んでください。
• ※ その他の駆動方法における負荷トルクの計算式については、技術資料に掲載しています。

負荷トルクの算出には、運転方向荷重（F）の計算が必要です。
傾斜角αが存在する場合は、テーブルとワークの総重量（m）や
重力加速度（g）を考慮してください。

\(\bbox[8pt, border: 1px solid black]{\begin{align} \text { 運転方向荷重 }F=F_A+mg\ (\sin \alpha+\mu \cos \alpha)\ [\mathrm{N}]\end{align}}\)

傾斜がある場合でも計算できるよう、三角関数を用いています。
傾斜角が水平、または垂直の場合は、右の表にある値を代入し、計算してください。

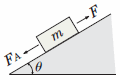
参考	水平駆動（α = 0°）	sinα = 0
		cosα = 1
	垂直駆動（α = 90°）	sinα = 1
		cosα = 0

さらに、ボールねじ機構を使用する場合、運転方向荷重（F）の算出のほかに、予圧荷重（F₀）の計算が必要です。
予圧荷重は、一般的に以下の値が目安とされています。（※ 詳しい値は、ボールねじメーカーへお問い合わせください。）

• ※ 摩擦係数は、ガイドの有無によって値が異なります。以下の値をご参考にしてください。

ガイド有	摩擦係数 ： 0.05 ～ 0.1	ガイド無	摩擦係数 ： 0.1 ～ 0.3

負荷トルクの計算例

手順

① 運転方向荷重を求める

② 予圧荷重を求める ※ ボールねじ駆動のみ

③ 負荷トルクを求める

ボールねじ駆動

機構条件の一覧を表示する

運転方向荷重（F）を求める

機構条件をもとに、運転方向荷重（F）を求めます。

\(\begin{align} \text { 運転方向荷重 }F & = F_A+mg\ (\sin \alpha+\mu \cos \alpha)\\[ 5pt ] & = 0\ [\mathrm{N}]\ + 27.5 [\mathrm{kg}]\times \ 9.807\ [\mathrm{m} / \mathrm{s}^2] (\sin 0^{\circ}+\ 0.05 \cos 0^{\circ})\\[ 5pt ] & = 13.5\ [\mathrm{N}]\end{align}\)

機構条件

• F_A （外力） ： 0 [N]
• m （テーブルとワークの総重量） ： 27.5 [kg]
• g （重力加速度） ： 9.807 [m/s²]
• α （傾斜角度） ： 0 [°]
• µ （摺動面の摩擦係数） ： 0.05

予圧荷重（F₀)を求める

運転方向荷重（F）の値をもとに、予圧荷重（F₀)を求めます。

\(\bbox[8pt, border: 1px solid black]{\begin{align} \text { 予圧荷重 }F_0= \frac{F}{3}\ = \frac{13.5\ [\mathrm{N}]}{3}\ =\ 4.5\ [\mathrm{N}]\end{align}}\)

負荷トルク（T_L)を求める

機構条件と、運転方向荷重（F）・予圧荷重（F₀)の値をもとに、負荷トルク（T_L)を求めます。

\(\begin{align} \text{負荷トルク }T_L & = \left[\frac{F\cdot P{_B}}{2 \pi \cdot \eta} + \frac{\mu_0 \cdot F_0 \cdot P_B}{2 \pi}\right]\\[ 5pt ] & = \frac{13.5\ [\mathrm{N}]\ \times\ ( 20 \times 10^{-3})[\mathrm{m}]}{2\pi\ \times\ 0.9} + \frac{0.3\ \times\ 4.5\ [\mathrm{N}] \times\ ( 20 \times 10^{-3})[\mathrm{m}]}{2\pi}\\[ 5pt ] & =\ 0.0520\ [\mathrm{N} \cdot \mathrm{m}] \end{align}\)

機構条件

• P_B（ボールねじのリード） ： 20 [mm]
• µ₀ （予圧ナットの摩擦係数） ： 0.3
• η （効率） ： 0.9

タイミングベルト・プーリー駆動

機構条件の一覧を表示する

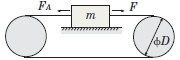
運転方向荷重（F）を求める

機構条件をもとに、運転方向荷重（F）を求めます。

\(\begin{align} \text { 運転方向荷重 }F & = F_A+mg\ (\sin \alpha+\mu \cos \alpha)\\[ 5pt ] & = 0\ [\mathrm{N}]\ + 3.5 [\mathrm{kg}]\times \ 9.807\ [\mathrm{m} / \mathrm{s}^2] (\sin 0^{\circ}+\ 0.05 \cos 0^{\circ})\\[ 5pt ] & = 1.72\ [\mathrm{N}]\end{align}\)

機構条件

• F_A （外力） ： 0 [N]
• m （テーブルとワークの総重量） ： 3.5 [kg]
• g （重力加速度） ： 9.807 [m/s²]
• α （傾斜角度） ： 0 [°]
• µ （摺動面の摩擦係数） ： 0.05

負荷トルク（T_L)を求める

機構条件と、運転方向荷重（F）の値をもとに、負荷トルク（T_L)を求めます。

\(\begin{align} \text { 負荷トルク } {T_L} & =\frac{{F} \cdot {D}}{2 \cdot \eta} \\[ 5pt ] & =\frac{1.72\ [\mathrm{N}] \times 31.85 \times 10^{-3}\ [\mathrm{m}]}{2 \times 0.9} \\[ 5pt ] & =0.0304\ [\mathrm{N} \cdot \mathrm{m}] \end{align}\)

機構条件

• D （プーリーの直径） ： 31.85 ×10^-3 [m/rev]
• η （効率） ： 0.9

次のページでは、装置の負荷慣性モーメントを求めます。